Дизеринг с распределением коррекции

В прошлой части мы рассмотрели имитацию полутонов (дизеринг) с помощью шаблона, который обладает несколькими недостатками:

1. Количество передаваемых оттенков ограничено размером матрицы
2. Каждый оттенок создается хорошо различимым регулярным узором, что может не очень хорошо смотреться на фотографиях
3. На изображениях с плавным переходом полутонов будут видны четкие границы узоров
4. Тонкие линии контрастного цвета могут пропасть полностью, если попадутся на неудачный участок шаблона

Для борьбы с этими недостатками был придуман другой метод, заключающийся в адаптивном распределении значения коррекции, возникшего при приведении клеточки к черному или белому цвету, на соседние клеточки.

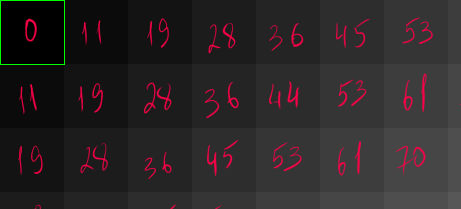
За основу возьмем то же самое изображение 16x16 клеточек из предыдущей части:

Если дизеринг по шаблону при сохранении общего принципа алгоритма использует для создания полутонов шаблоны (матрицы), то дизеринг с распределением коррекции (ошибки) работает с фильтрами, которые указывают, какую часть коррекции на какие именно соседние клеточки необходимо распределить.

Фильтров придумано огромное множество и они создают разные эффекты. Одним из самых распространенных фильтров является фильтр Флойда-Штейнберга, который выглядит следующим образом:

-1	-1	7/16
3/16	5/16	1/16

Здесь голубым цветом выделена исходная клеточка, которую мы модифицируем и с которой распределяем коррекцию на соседние клеточки, красным - клеточка, на которую мы не распространяем коррекцию, а зеленым - клеточки, на которые распространение коррекции происходит.

Знаменатель дроби означает, на сколько частей нужно разделить значение коррекции, а числитель - какая доля коррекции будет распределена. Упрощенно можно считать, что если сумма всех числителей будет равна знаменателю, то полученный результат коррекции будет примерно совпадать с исходным изображением по яркости и контрасту. Если сумма числителей будет меньше знаменателя, то картинка станет более контрастной, потеряются оттенки в самых светлых и самых темных участках. Если больше, то картинка станет ярче.

Как мы видим из таблички, в фильтре Флойда-Штейнберга распространение коррекции происходит вправо, вниз, по диагонали вправо-вниз и влево-вниз. Есть фильтры, которые распространяют коррекцию не только на непосредственно соседние клеточки, но и через одну или даже дальше. Например, фильтр Сьерры выглядит следующим образом:

-1	-1	-1	5/32	3/32
2/32	4/32	5/32	4/32	2/32
-1	2/32	3/32	2/32	-1

Почему распространение коррекции идет вправо и вниз и не затрагивает клеточки слево от текущей? Дело в том, что обработка изображения идет сверху вниз и слева направо, и слева от текущей клеточки у нас расположены уже обработанные, то есть либо черные, либо белые клеточки. Если на них распространить коррекцию, то они приобретут оттенок серого цвета и их придется обрабатывать повторно. Есть более сложные алгоритмы, которые умеют работать с распределением коррекции на уже обработанные ранее клеточки, но они за рамками данной статьи.

Итак, давайте попробуем обработать нашу картинку алгоритмом дизеринга с распространением коррекции, используя фильтр Флойда-Штейнберга.

Берем первую клеточку. Она уже черного цвета, поэтому делать тут нечего.

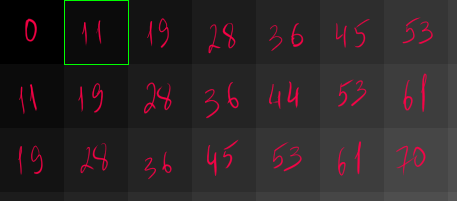
У следующей клеточки оттенок серого с яркостью 11. Это меньше порогового значения 128, поэтому мы приведем ее к черному, т.е. к 0. В результате у нас возникнет значение коррекции в 11 единиц, которое нам нужно распределить на соседние клеточки в соответствии с фильтром. Знаменатель дроби (количество долей) у нас 16, поэтому делим 11 на 16 и получаем размер одной доли - 0,6875. Вправо мы должны распределить 7 долей, т.е. 4,8125. Яркость правой клеточки у нас 19, прибавим к ней 4,8125, округлим математически до целого значения и получится новое значение яркости - 24:

Вправо и вниз мы распределяем 1 долю, т.е. 0,6875, или округленно 1:

Вниз распределяем 5 долей, т.е. 3,4375, округленно 3:

И влево-вниз 3 доли, т.е. 2,0625, округленно 2:

Переходим ко второй клеточке. Ее значение яркости уже не 19, а 24, но это все еще меньше 128, поэтому клеточку приводим к черному цвету (0) и получаем значение коррекции 24, которое нужно распределить вправо, вправо-вниз, вниз и влево-вниз соответственно на 11, 2, 8 и 5 значений:

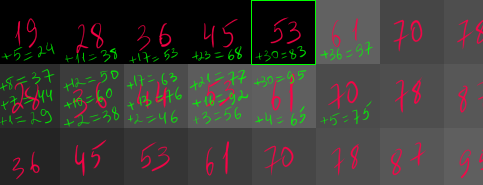
Четвертую клеточку мы тоже приводим к черному и распределяем уже 38 пунктов коррекции:

Пройдем до конца ряда:

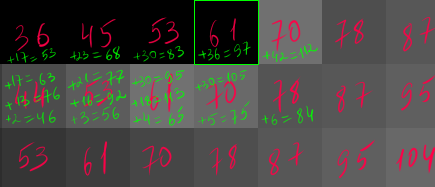
Обратите внимание, как постепенно накапливается значение коррекции, высветляя соседние клеточки все больше и больше, пока не приводит к тому, что очередную клеточку мы уже приводим не к черному, а к белому: 143 -> 255. При этом значение коррекции у нас уже становится отрицательным: 143 - 255 = -112, соответственно соседние клеточки мы уже будем распределением коррекции не высветлять, а затемнять, отнимая яркость в соответствии с долями распределения коррекции:

Теперь посмотрим на видео, как происходит обработка картинки от начала до конца: